4 線形回帰モデル

　今回のゴールは、入出力間の関係をより一般的な表現が可能な線形回帰モデルを導出することである。まず、単回帰モデルを拡張した重回帰モデルを定義し、最小二乗法によってパラメータを推定するベクトル表現を導出する。続いて入力空間を特徴空間に写像した特徴ベクトルに対して重回帰モデルを適用することによって線形回帰モデルを導くこととする。

4.1 重回帰モデル

　\(\ D \ \)次元空間における観測値集合 \(\ {\cal D}=\{\,({\bf x}_i,y_i)\,|\,{\bf x}_i \in {\mathbb R}^D \ ,\ y_i\in \mathbb{R}\ ,\ i=1,\cdots ,n\,\} \ \) が与えられたとき、モデルの回帰値\(\ \hat{y} \ \)を入力ベクトル\(\ {\bf x} \ \)と重みベクトル\(\ {\bf w}=(w_0, w_1,\cdots ,w_D)\TP \ \)で定義される次式によって関係付けるのが重回帰モデルである。 \[ \hat{y}=w_0 +w_1 x_1+w_2 x_2+\cdots +w_Dx_D \tag{4.1} \] 　以下、次式で示される回帰値\(\ {\hat y}_i \ \)と観測値\(\ y_i \ \)の間の誤差の平方和\(\ {\varDelta} \ \)を最小にする\(\ {\bf w} \ \)を最小二乗法で求める。 \begin{eqnarray} \varDelta &=& \sum_{i=1}^n {(y_i-(w_0 +w_1 x_{i1}+w_2 x_{i2}+\cdots w_Dx_{iD}))^2} \tag{4.2} \\ \frac{\partial{\varDelta}}{\partial{{\bf w}}}&=&{\left(\frac{\partial{\varDelta}}{\partial{w_0}} \ ,\ \frac{\partial{\varDelta}}{\partial{w_1}}\ ,\ \cdots \ ,\ \frac{\partial{\varDelta}}{\partial{w_D}}\right)}\TP = {\bf 0} \tag{4.3} \end{eqnarray} 　ここで、式 (4.2) 和をベクトルの内積で表すこととする。 \[ \hat{y}=w_0 \cdot 1 +w_1\cdot x_1+w_2\cdot x_2+\cdots +w_D \cdot x_D = {\bf w}\TP \lower 3em {\pmatrix{1 \\ x_1 \\ x_2 \\ \vdots \\ x_D}} \tag{4.4} \] 　入力ベクトルを拡張した行ベクトル\(\ {\bf x}=(1,x_1,x_2,\cdots ,x_D )\TP \ \)を行方向に配列した\(\ n \times (D+1) \ \)行列を定義する。 \[ X=\pmatrix{1 & x_{11} & x_{12} & \cdots & x_{1D} \\ 1 & x_{21} & x_{22} & \cdots & x_{2D} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nD}} \tag{4.5}\] 　式 (4.2) で表される誤差の平方和\(\ \varDelta \ \)をベクトル形式で求めると \begin{eqnarray} {\varDelta}&=&\sum_{i=1}^n (y_i-\hat{y}_i)^2=\sum_{i=1}^n(y_i-{\bf w}\TP {\bf x}_i)^2 \\ &=&({\bf y}-X{\bf w})\TP ({\bf y}-X{\bf w}) ={\bf y}\TP {\bf y}-2{\bf w}\TP (X{\bf y})+{\bf w}\TP X\TP X{\bf w} \end{eqnarray} となる。ここで、ベクトルの１次形式と２次形式の微分に関する公式 \begin{eqnarray} \frac{\partial}{\partial{{\bf w}}}{\bf w}\TP {\bf x}&=&{\bf x} \\ \frac{\partial}{\partial{{\bf w}}}{\bf w}\TP X{\bf w}&=&(X+X\TP ){\bf w} \end{eqnarray} を用い、さらに\(\ X\TP X \ \)が対称行列であることから \begin{eqnarray} \frac{\partial{}\varDelta}{\partial{{\bf w}}}&=&-2X\TP {\bf y}+(X\TP X+(X\TP X)\TP ){\bf w} \\ &=&-2X\TP {\bf y}+2X\TP X{\bf w} \end{eqnarray} が得られる。この結果と式 (4.3)の停留条件から重回帰モデルについて正規方程式のベクトル表現を導出できる。 \[ X\TP X{\bf w}=X\TP {\bf y} \tag{4.6} \] 　対称行列\(\ X\TP X \ \)の逆行列が存在すれば、 \[ {\bf w}=(X\TP X)^{-1}X\TP {\bf y} \tag{4.7} \] によってパラメータを求めることができる。パラメータが確定すると、\(\ X \ \)に対する回帰値\(\ \hat{{\bf y}} \ \)は \[ \hat{{\bf y}}={X\bf w} \tag{4.8} \] と表すことができ、\(\ X \ \)は重みベクトル\(\ {\bf w} \ \)から回帰値ベクトル\(\ \hat{{\bf y}} \ \)を生成する計画行列と呼ぶ。

4.2 重回帰モデルの解釈

　重回帰モデルにおいて、特に\(\ D=1 \ \)のときには単回帰モデルを表すことになり、式 (4.6) から親しみのある正規方程式 \[ \pmatrix{{n}& {\sum_{i=1}^n x_i}\\{\sum_{i=1}^n x_i} &{\sum_{i=1}^n x_i^{\, 2}}}\pmatrix{w_0 \\ \lower 0.5em{w_1}}=\pmatrix{{\sum_{i=1}^n y_i} \\{\sum_{i=1}^n x_iy_i} } \tag{4.9} \] が得られる。
　また、重回帰モデルにより得られる回帰値\(\ \hat{y} \ \)は、\(\ (D+1) \ \)次元空間における\(\ D \ \)次元の超平面上の点であり、超曲面を表現することはできない。しかし、１次元入力でなじみのある多項式回帰モデルを実現するためには、\(\ {\bf x}=(1,x,x^2,\cdots ,x^N)\TP \ \)に対して重回帰モデルを適用すれば実現できる。このことからより一般的な多次元入力についても重回帰モデルを適用できることを示唆している。 　

4.3 線形回帰モデル

　前節では１次元の入力\(\ x \ \)のべき乗項で構成するベクトルに対して重回帰モデルを適用したが、このアプローチを以下のように拡張することで、回帰モデルを一般化することができる。すなわち、\(\ D \ \)次元の入力ベクトル\(\ {\bf x} \ \)を\(\ N \ \)次元の特徴空間に写像する基底関数\(\ \phi_i({\bf x}) \ \)を考える。\(\ N \ \)個の基底関数により入力\(\ {\bf x} \ \)を写像して得られるベクトル \[ {\boldsymbol \phi}({\bf x}) = (\phi_1({\bf x}),\phi_2({\bf x}),\cdots, \phi_N({\bf x}))\TP \tag{4.10}\] に対して重回帰モデルを適用すればよい。式 (4.10) のベクトルを\(\ N \ \)次元の特徴空間における特徴ベクトルと呼び、暗黙のうちに\(\ \phi_1({\bf x})\equiv1 \ \)と考える。
　\(\ n \times N \ \)計画行列を次式で定義し \[ \Phi=\pmatrix{\boldsymbol\phi({\bf x}_1)\TP \\ \boldsymbol\phi({\bf x}_2)\TP \\ \vdots \\ \boldsymbol\phi({\bf x}_n )\TP }= \pmatrix{\phi_1({\bf x}_1) & \phi_2({\bf x}_1) &\cdots & \phi_N({\bf x}_1) \\ \phi_1({\bf x}_2) & \phi_2({\bf x}_2) & \cdots & \phi_N({\bf x}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1({\bf x}_n) & \phi_2({\bf x}_n) & \cdots & \phi_N({\bf x}_n) \tag{4.11}}\] 式 (4.6) の\(\ X \ \)を\(\ \Phi \ \)に置き換えることで、線形回帰モデルの正規方程式 \[ \Phi\TP \Phi{\bf w}=\Phi\TP {\bf y} \tag{4.12} \] が得られる。
　逆行列\(\ (\Phi\TP \Phi)^{-1} \ \)が存在すれば\(\ N \ \)次元の重みベクトル、 \[ {\bf w}=( \Phi\TP \Phi)^{-1}\Phi\TP {\bf y} \tag{4.13} \] 回帰値ベクトルは、 \[ \hat{{\bf y}}=\Phi{\bf w} \tag{4.14} \] によって求めることができる。
　式 (4.14) が意味することは、計画行列\(\ \Phi \ \)は定数行列であるので、回帰値ベクトルは重みベクトルの線形変換で表されることである。
　図 4.1 に線形回帰モデルを構成する３つの空間であるデータ空間、特徴空間、パラメータ空間の関係を示す。

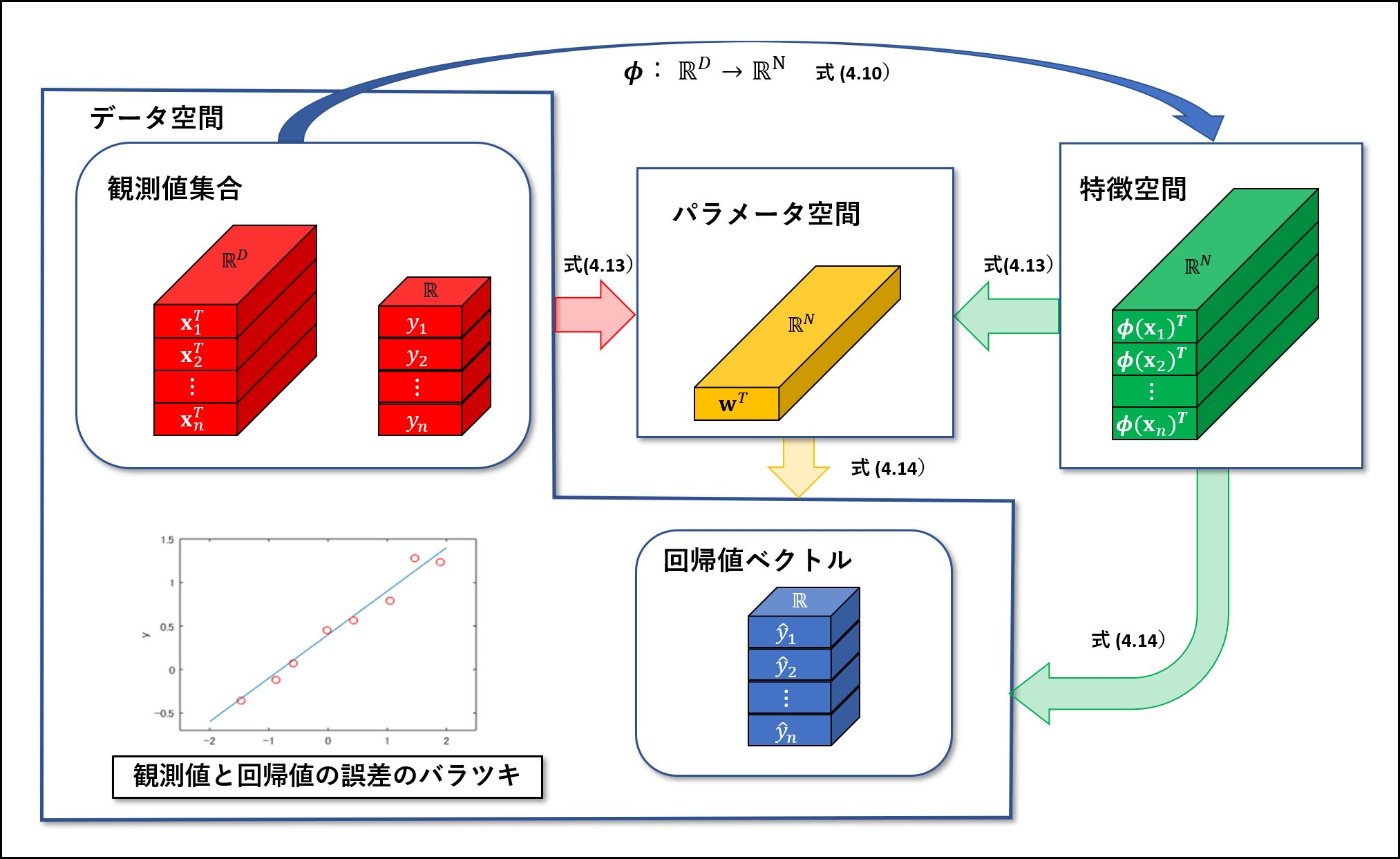
　単回帰から始めて、柔軟かつ一般的な線形回帰モデルが導かれた。しかし、基底関数をどのように選択すれば良いか、また確率モデルをどのように構成すれば良いかなど新たな課題が浮かび上がってくる。
　次回、線形回帰モデルを確率モデルとして考えるためのアプローチを紹介する。