モノづくりと不確かさの定量化（第9回）ガウス過程回帰を支える実験計画法
9 ガウス過程回帰を支える実験計画法
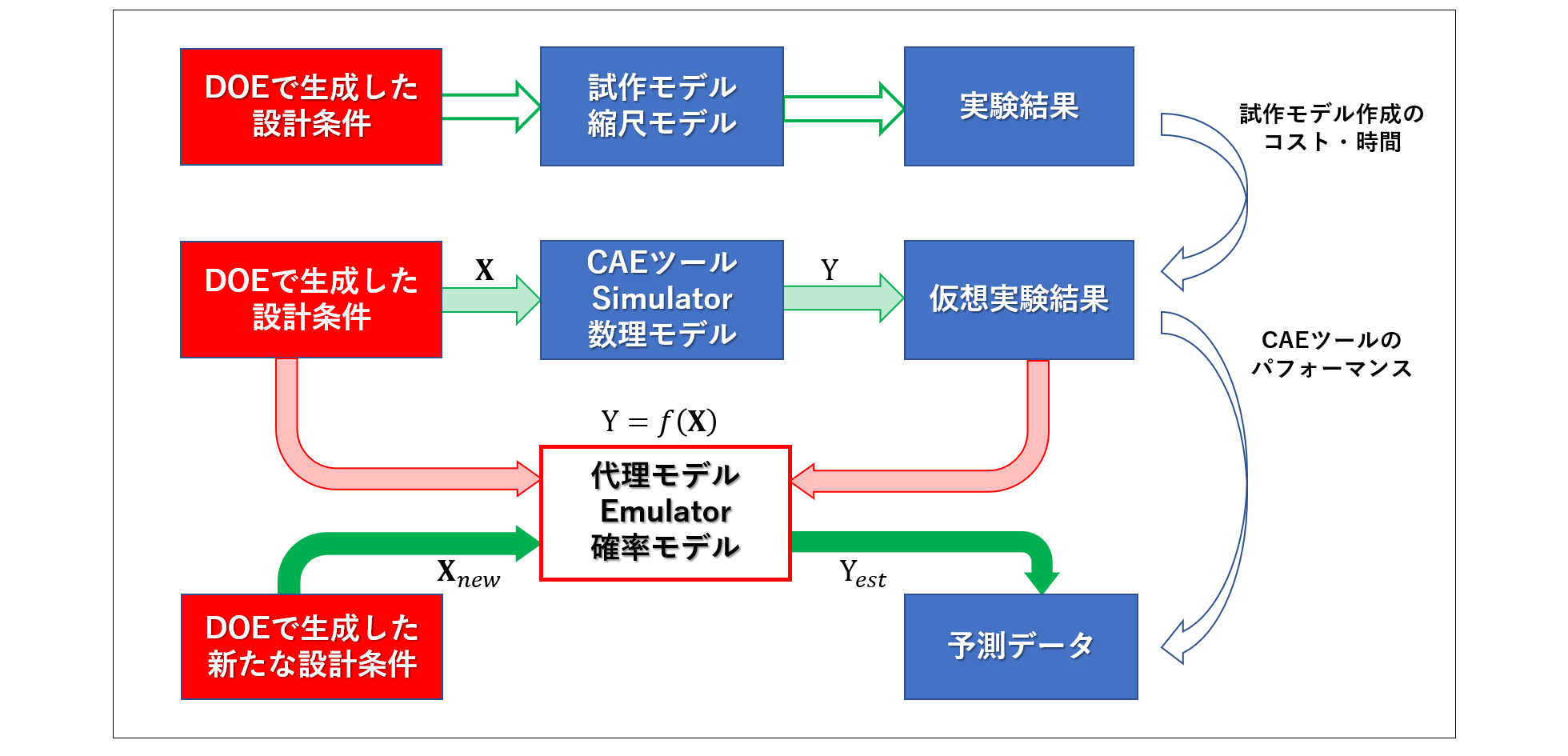
前回までに、「観測値集合から柔軟な回帰モデルの関数\(\ y=f({\bf x})\ \)を推定する確率モデル」であるガウス過程回帰を紹介した。この強力なツールを有効活用するためには、観測値集合\(\ {\cal D} = \{\,({\bf x}_i,y_i)\,|\, i = 1, \cdots ,N,{\bf x}_i \in \RR ^D\}\,\ \)を効率的に求めるシナリオが必要となる。
ガウス過程回帰の振舞いはカーネル行列に支配され、その要素は入力\(\ {\bf x}_i\ \)と\(\ {\bf x}_j\ \)のカーネル関数\(\ k({\bf x}_i,{\bf x}_j)\ \)で構成された。このことから、「\( \ D \ \)次元空間における\(\ N\ \)個の入力をどのように選択すれば効率的にかつ合理的に確率モデルを推定できるか」という問題を解くことに帰結する。
著名な統計学者フィッシャー（R. Fisher）が提案した実験計画法（design of experiments, DOE）の構成要素である直交表、そして直交表をより柔軟な手法に拡張したラテン超方格サンプリング（Latin hypercube sampling）がこの問題への解決手段となる。
9.1 直交表
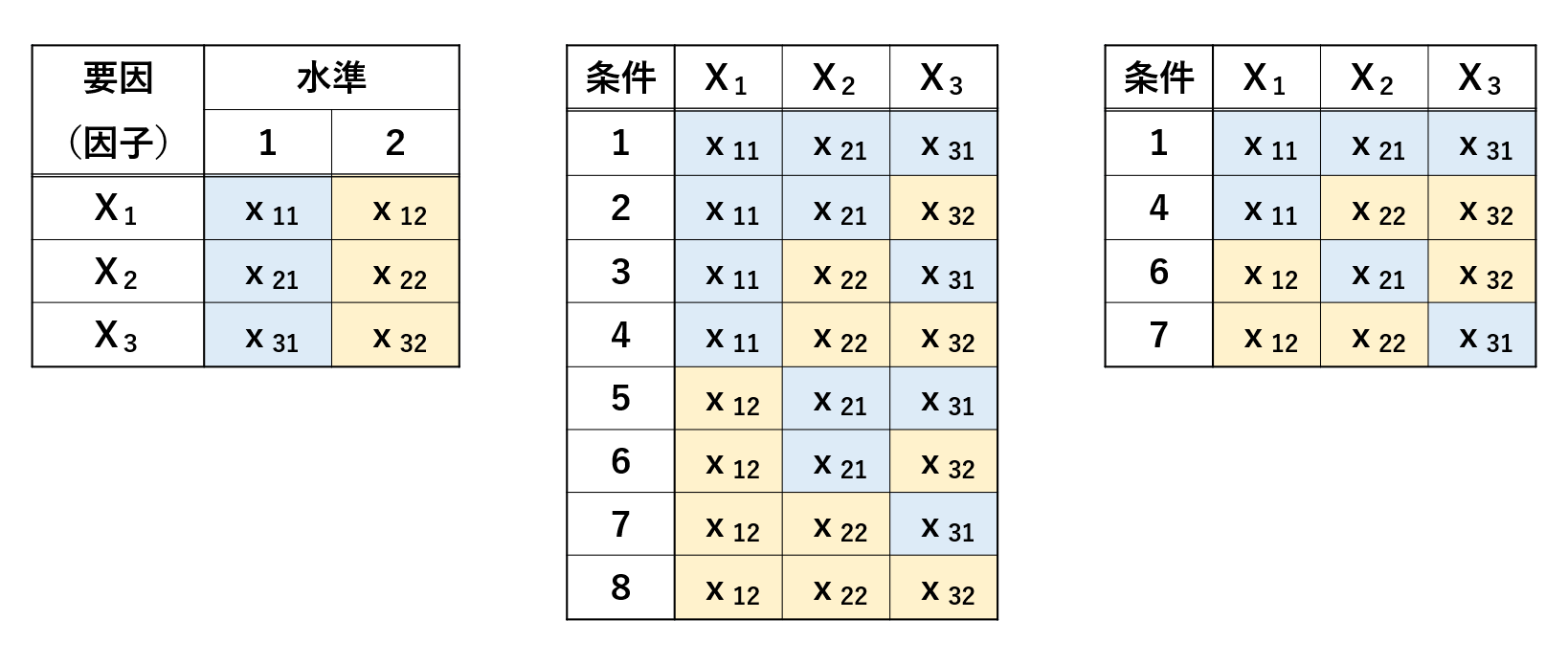
実験計画法の出発点となった直交表について、\(\ D=3\ \)の場合を例として紹介する。
ガウス過程回帰への入力に相当する条件を設定できる３つの項目を要因（因子）と呼び、それぞれの要因ごとに２つの条件（水準という）が選択できると想定すると（図 9.2 左）、入力条件の組合せは\(\ 2^3=8\ \)通り（図 9.2 中央）となる。図 9.2 右に示す直交表は、４通りの組合せを考えれば各要因の水準が２つ現れていることが分かり、少ない入力条件で効率的かつ合理的な条件設定が可能であることを示唆している。この直交表を\( \ L_4(2^3) \ \)と表す。直交表にはこのほかに、2水準-7要因を8通りの条件で設定できる\(\ L_8(2^7)\ \)、3水準-4要因を9通りの条件で設定できる\(\ L_9(3^4)\ \)などが提案されている。
9.2 ラテン超方格サンプリング
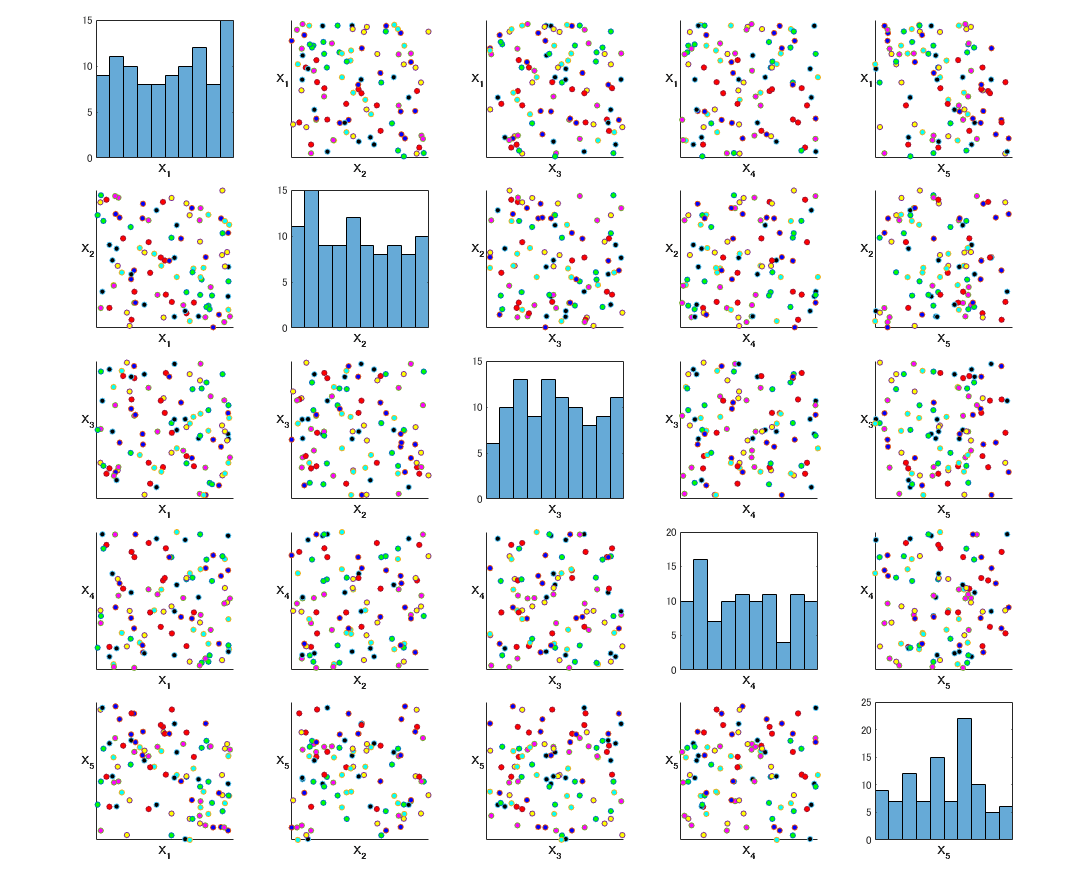
要因数\(\ D=5\ \)の場合を例に、\(\ N=100\ \)組のデータで実験計画法を実現することを想定する。それぞれの要因について設計条件の下限値と上限値で正規化した\(\ [0,1]\ \)の乱数を発生させた場合、直交性がどの程度実現できるかを確かめる。5次元の一様乱数発生器（例えば、MATLABのrand関数）によるいわゆるモンテカルロ法サンプリングを実施した結果を図 9.3 に示す。２要因間の分布を表す20組の散布図と各要因の分布を0.1幅の\(\ \sqrt{N}=10\ \)個の階級の頻度で表したヒストグラムをまとめて表示している。
散布図からは一見して読み取ることはできないが、ヒストグラムからは（特に\(\ X_5\ \)）直交性が担保されていないことが分かる。
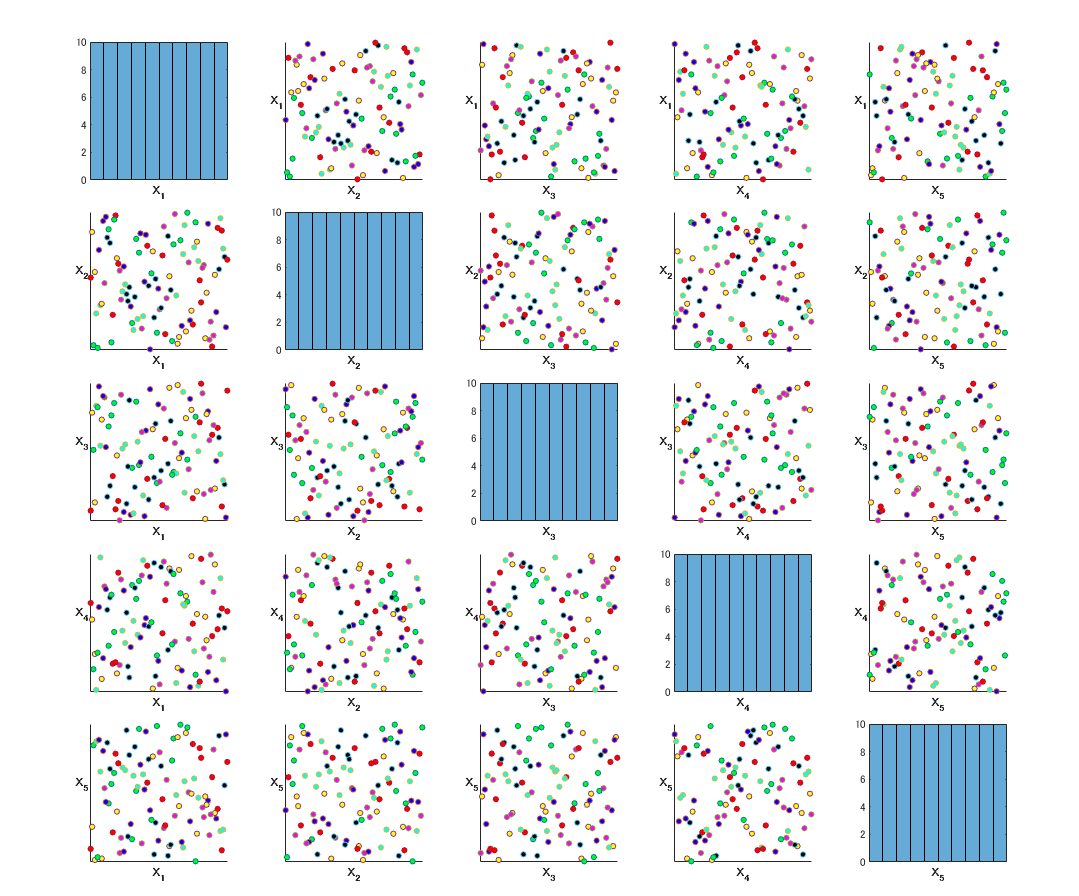
繰り返しになるが、モノづくりのライフサイクルにおいて、「性能・品質・コスト」のバラツキを試作モデルを作成することなく予測できる強力なツールを入手したことになる。
9.3 おわりに
これまで、モノづくりの設計現場においてガウス過程回帰がどのように役立つかをメインテーマとしてきた。しかし、ガウス過程は回帰問題だけではなく、分類問題や機械学習分野にも適用することができるツールである。以下に参考文献を紹介する。
入門：持橋大地, 大羽成征, ガウス過程と機械学習, 講談社(2019)
中級：Rasmussen C.E, and Wiliams C.K.I., Gaussian Process for Machine Learning, MIT Press (2006) 日本語版あり
上級：Bishop C.M., Pattern Recognition and Machine Learning, Springer(2006) 日本語版あり
次回は最終回として、ガウス過程の計算パッケージについて紹介する。