6 ガウス過程
前回は、線形回帰モデルの重みと出力を確率変数として扱う確率モデルを紹介した。今回のゴールは、確率過程の概念を紹介することであり、特に多変量正規分布(multivariate normal distribution)を採用した確率モデルであるガウス過程(Gaussian process)を紹介する。
ガウス過程は線形回帰モデルで重要な役割を果たしていた重みベクトル\(\ {\bf w}\ \)を積分消去した確率モデルであり、パラメータ空間ではなく関数空間における確率変数の振舞いを考えることになる。一方で、ガウス過程をランダムな関数を発生させる確率分布と見做すこともでき、より柔軟な回帰モデルを構築することができる。
6.1 基底関数と正規分布
線形回帰モデルでは、回帰値は式 (6.1) で示すように基底関数ベクトル\(\ \BS(\phi) ({\bf x})\ \)と重み\(\ {\bf w}\ \)の線形結合で表され、基底関数の選択には自由度があった。
\[y= {\bf w}\TP \BS(\phi) ({\bf x}) \tag{6.1}\]
ここで、基底関数として等間隔のグリッド\(\ \mu_h\ \)の上で定義された正規分布(正規化係数は省略)を選択することを考える。
\[\phi_h(x)=\exp\left(-\frac{(x-\mu_h)^2}{2{\scr l}^2} \right)\ ,\quad \mu_h \in \{-H,\cdots , -1,0,1,\cdots ,H\} \tag{6.2}\]
この関数を動径基底関数(radial basis function, RBF)といい、標準偏差\(\ \sigma\ \)に対応する\(\ {\scr l}\ \)を特性長スケール(characteristic length scale)という。
因みに、\(\ \phi(x) = \mathrm{sinc}\, (x)={\sin (\pi x)}/{\pi x}\ \)は、等間隔時間でサンプリングした時系列信号がサンプリング定理を満たすとき、元の信号を復元するための基底関数であることが知られている。
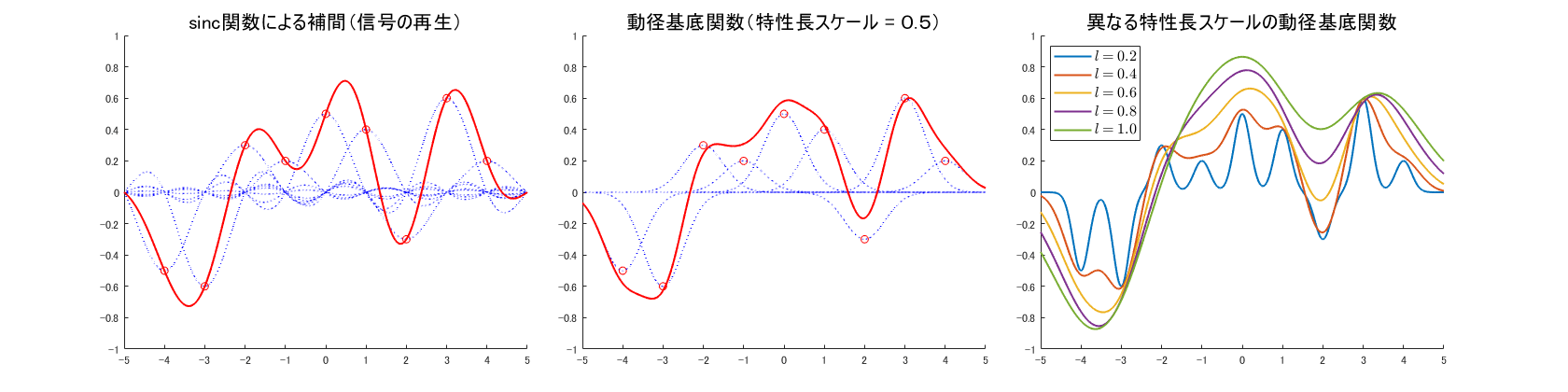
一例として、9点の重みベクトル\(\ {\bf w}=(-0.5,-0.6,0.3,0.2,0.5,0.4,-0.3,0.6,0.2)\TP \ \)を想定し、異なる基底関数により回帰曲線を求めた結果を図 6.1 に示す(青色点線:重み付けされた基底関数)。図 6.1(左)は\(\ {\rm sinc}\ \)関数による補間ですべてのグリッド点における重み(赤丸)を通る滑らかな曲線が一意に定まる。図 6.1(中央)は特性長スケールが\(\ 0.5\ \)のときの動径基底関数による回帰曲線であり、グリッド点を少し外れてはいるものの大局的には滑らかな回帰曲線が得られている。図 6.1(右)は、異なる特性長スケールの動径基底関数による回帰曲線を示している。特性スケール長が小さいときには回帰曲線は振動的になり、逆に大きな特性長スケールに対しては非常に滑らかな回帰曲線が得られることが分かる。
以上のことから線形回帰モデルの基底関数として、目的に応じて適切な特性長スケールの動径基底関数を選択することがガウス過程への第一歩となることが示唆される。
6.2 次元の呪い
基底関数選択の自由度の壁を排除したものの、次元の呪いと呼ばれる新たな高い障壁が出現する。図 6.1 の例は、入力が1次元の場合であったが、高次元の入力の場合には1次元当たりのグリッド数が 9 であっても基底関数の数は指数関数的に増加する。4次元では\(\ 9^4=6,561\ \)個、10次元では\(\ 9^{10}=3,486,784,401\ \)個もの基底関数が必要となる。
加えて、等間隔のグリッドを前提とすることは、入力の自由度を大きく制約することになる。これらの新たな壁を克服するための確率モデルがガウス過程である。
6.3 ガウス過程の導入
6.3.1 簡単なガウス過程
線形回帰モデルでは、回帰値ベクトルは重みベクトルを定数行列である計画行列による線形変換\(\ \hat{\bf y}=\Phi\bf w \ \)として求められることを示した。ここで、以下の2つの前提を置くことで出力の確率分布から重みベクトルが積分消去できることを示す。第1の前提は、出力にノイズが重畳していないこと、そして第2の前提は重みベクトルが平均値\(\ {\bf 0}\ \)、共分散行列が\(\ \Sigma_p\ \)の正規分布に従うとすることである。
\begin{cases}
{\bf y} = \hat{\bf y} \\
\lower 0.5em { {\bf w} \sim {\cal N} ({\bf 0},\Sigma_p)} \\
\tag{6.3}
\end{cases}
重みベクトル\(\ \bf w\ \)が正規分布に従うので、線形変換された出力\(\ \bf y \ \)も正規分布の再生性により正規分布に従うことになる。従って期待値は
\[\EV({\bf y} ) = \EV(\Phi {\bf w} ) = \Phi \EV({\bf w}) = {\bf 0} \tag{6.4} \]
また、共分散行列は
\begin{eqnarray}
\Sigma &=& \EV({\bf y}{\bf y}\TP ) – \EV({\bf y}) \, \EV(\bf y) \TP = {\mathbb E} \left[(\Phi {\bf w})(\Phi {\bf w})\TP \right] \\
&=& \Phi {\mathbb E}\left[{\bf w}{\bf w}\TP \right] \Phi\TP = \Phi \Sigma_p \Phi \TP \tag{6.5}
\end{eqnarray}
となり、\(\ \bf y\ \)は多変量正規分布に従うことが示される。
\[{\bf y} \sim {\cal N}({\bf 0},\Phi \Sigma_p \Phi \TP ) \tag{6.6}\]
式 (6.6) では重みベクトルが期待値を求める積分によって消去され、入力の特徴ベクトルによって構成される計画行列と特徴ベクトルが主役となる。
式 (6.6) の\(\ (n \times n)\ \)共分散行列を\(\ K\ \)とすると、その\(\ (i,j)\ \)成分を次式の共分散関数で表すこととする。
\[k({\bf x}_i,{\bf x}_j)=\BS(\phi) ({\bf x}_i)\TP \Sigma_p \,\BS(\phi) ({\bf x}_j) \tag{6.7}\]
6.3.2 カーネルトリック
式 (6.7) の共分散行列\(\ \Sigma_p\ \)は、正値行列でありかつ対称行列であるので、ユニタリ行列\(\ U\ \)によって正の固有値\(\ \lambda_i^{\,2}\ \)をもつ行列\(\ D\ \)に対角化できることが知られている。 \[\Sigma_p = UDU\TP \ , \quad D_{ij}= \begin{cases}\lambda_i^{\,2} & i=j \\ 0&i\ne j \end{cases} \tag{6.8}\] そこで、対称行列\(\ \Sigma_p^{\,1/2}=UD^{1/2}U\TP \ \)によって式 (6.7) を変形すると \[ k({\bf x}_i,{\bf x}_j)=\BS(\phi) ({\bf x}_i)\TP \Sigma_p^{\,1/2} \Sigma_p^{\,1/2} \,\BS(\phi) ({\bf x}_j) =\left( \Sigma_p^{\,1/2}\BS(\phi) ({\bf x}_i) \right) \TP \left( \Sigma_p^{\,1/2}\BS(\phi) ({\bf x}_j) \right) \tag{6.9}\] が得られる。\(\ \Sigma_p^{\,1/2}\ \)は定数行列であるので線形変換\(\ \BS(\psi) ({\bf x})=\Sigma_p^{\,1/2}\BS(\phi) ({\bf x}) \ \)によって共分散関数を次式のようにベクトルの内積として表すことができる。 \[k({\bf x}_i,{\bf x}_j)= \BS(\psi) ({\bf x}_i)\TP \BS(\psi) ({\bf x}_j)= \BS(\psi) ({\bf x}_i) \cdot \BS(\psi) ({\bf x}_j) \tag{6.10}\] 特徴空間において特徴ベクトル\(\ \BS(\phi) ({\bf x})\ \)を陽な形式で求めず、データ空間で定義される内積\(\ k({\bf x}_i,{\bf x}_j)\ \)で共分散行列を構成する方法をカーネルトリック(kernel trick)といい、\(\ k({\bf x}_i,{\bf x}_j) \ \)をカーネル関数、次式で定義される行列\(\ K\ \)をカーネル行列という。 \[K_{ij} = k({\bf x}_i,{\bf x}_j) \tag{6.11}\]
6.3.3 カーネル関数の例
カーネル関数は目的に応じて様々な形式の関数が定義されているが、直感的には「入力\(\ {\bf x}\ \)が似ているときには、出力\(\ y\ \)も似ている」ことを表す関数である。代表的なカーネル関数が式 (6.2) を一般化した動径基底関数(RBF)である。 \[k({\bf x},{\bf x}’)=\theta_1 \exp \left( -\frac{|{\bf x}-{\bf x}’|^2}{\theta_2}\right)\tag{6.12}\] このカーネル関数は、\(\ {\bf x}\ \)と\(\ {\bf x}’\ \)との距離が短いときには大きな値となり、距離が遠いほど\(\ 0\ \)に近づくことがわかる。
6.4 ガウス過程の定義
関数\(\ f({\bf x})\ \)が以下の条件を満足するとき、\(\ f({\bf x})\ \)はガウス過程に従うという。
任意の自然数\(\ N\ \)について、入力\(\ {\bf x}_1,{\bf x}_2, \cdots ,{\bf x}_N \in {\cal X}\ \)に対する出力のベクトル \[ {\bf f}=(f({\bf x}_1),f({\bf x}_2), \cdots ,f({\bf x}_N))\] が、平均\(\ \BS(\mu) =(\mu({\bf x}_1),\mu({\bf x}_2), \cdots ,\mu({\bf x}_N))\ \)、\(\ K_{ij}=k({\bf x}_i,{\bf x}_j)\ \)を要素とする行列\(\ K\ \)を共分散行列とするガウス分布\(\ {\cal N}(\BS(\mu) ,K) \ \)に従う。
このとき、以下のように表す。 \[f({\bf x}) \sim {\cal GP} (\mu({\bf x}),k({\bf x},{\bf x}’)) \tag{6.13}\]
- 関数\( \ f({\bf x})\ \)は無限次元のベクトル\(\ {\bf f}\ \)である。
- しかし、有限個の入力に対する出力のガウス分布がガウス過程であり、無限次元のガウス分布を周辺化した\(\ N\ \)次元の多変量正規分布とも見做せる。
- カーネル関数と平均関数が決まると、ガウス過程は一意に決まる。
- 入力は図 6.1 のように等間隔に配列される必要はない。
- カーネル関数は、ランダムな関数を発生させる確率過程であり、ベイズ推定の枠組みにおける事前確率分布を与える。
- 観測値\(\ {\bf y}\ \)は予め平均値を引くことで\(\ {\BS(\mu) ={\bf 0}}\ \)とできるので、ガウス過程の性質は共分散行列\(\ K\ \)によってのみ一意に決まると考えることができる。式 (6.13) の正式な表現に代わり次式によってガウス過程で表すことがある。
6.5 観測ノイズの取り扱い
式 (6.3) では、出力にはノイズが含まれていないモデルを考えた。出力に次式に従うノイズ、 \begin{cases} y_n = f({\bf x}_n)+\epsilon_n \\ \lower 0.5em { \epsilon_n \sim {\cal N}(0,\sigma_n^{\,2})} \quad \quad n=1, \cdots ,N \tag{6.15} \end{cases} が重畳されている場合には、詳細の導出は省略するがカーネル関数は \[K_{ij}=k({\bf x}_i,{\bf x}_j)+\sigma_n^{\,2}\delta_{ij} \tag{6.16}\] で表される。ここで、\(\ \delta_{ij}\ \)は、\(\ i=j\ \)のときに\(\ 1\ \)、それ以外では\(\ 0\ \)となるクロネッカーのデルタである。すなわち、カーネル関数\(\ k\ \)で定まる共分散行列\(\ K\ \)の対角成分に、リッジ回帰と同様に\(\ \sigma_n^{\,2}\ \)を加えた行列として表される。
6.6 ガウス過程のまとめ
式 (6.12) において\(\ \theta_1=1.0\,,\ \theta_2=0.5\ \)としたカーネル関数によって生成された共分散行列(図 6.2 左)、区間\(\ [\,-4,4\,]\ \)を\(\ 0.01\ \)間隔で刻んだ\(\ 801\ \)点の入力から生成した共分散行列と式 (6.14) によってランダムに生成した5つの関数(図 6.2 中央)を示す。
図 6.2 (右) には、x 印で示す5点の観測データが与えられたとき、関数の事後分布の平均値と分散\(\ \sigma^2\ \)の平方根である標準偏差\(\ \sigma\ \)の\(\ \pm2\sigma \ \)の区間(信頼区間95%)を示した。この予測はガウス過程回帰(Gaussian process regression, GPR)と呼ばれる回帰モデルの推定結果であるが、その詳細は次回紹介する。
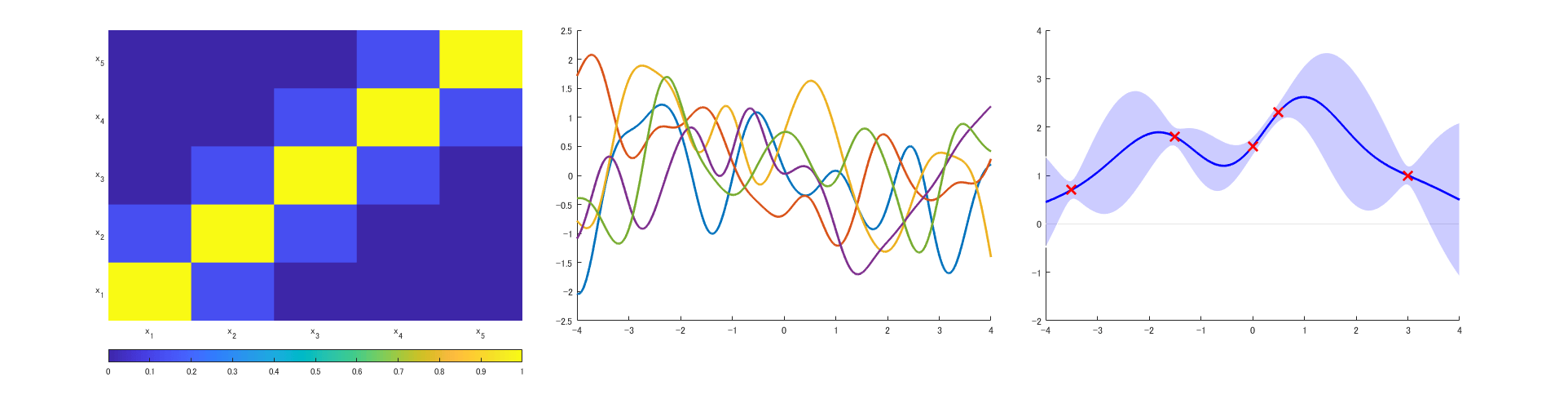
(左)共分散行列、(中央)ガウス過程からのサンプリングした5つの関数(右)予測分布
●モノづくりと不確かさの定量化(第5回)線形回帰モデルと確率モデル
https://kesco.co.jp/blog/4426/
●モノづくりと不確かさの定量化(第4回)線形回帰モデル
https://kesco.co.jp/blog/3844/
●モノづくりと不確かさの定量化(第3回)回帰モデルの導入
https://kesco.co.jp/blog/3171/
●モノづくりと不確かさの定量化(第2回)
https://kesco.co.jp/blog/3092/
●モノづくりと不確かさの定量化(第1回)
https://kesco.co.jp/blog/539/