連成解析
- ホーム >
- COMSOL Multiphysics >
- 連成解析
連成解析とは?
有限要素法における連成解析は、複数の物理現象が相互に影響しあう問題を一緒に解析する手法です。現実世界に即した最適設計を実現するには複雑な様々な物理現象の関連を定量的に検討する方法が良いと考えられます。例えば、太陽発電の効率改善を目標とすると、気象条件(地域ごとの年間日射量の差異)、気温(高温による太陽電池の効率低下)、降水量(汚れやホコリ、冷却効果など)、雲量(曇天時の発電効率)、太陽電池の素材(シリコン系や次世代ペロブスカイトや量子ドットなど)、パネルの設置構造(固定式、追尾式、角度・方位の制御)、風況(風による冷却、風による損傷、汚れ)、バッテリーや他のエネルギー貯蔵、といった具合に天候、地球規模・局地の相変化や流体運動、構造力学、化学・電気化学、量子力学が互いに連成しているシステムとして捉えた最適化が必要です。マルチフィジックス(多重物理連成)解析はこのような現実におこる複雑な数理工学問題を解決するために不可欠な手法であり、有限要素解析の汎用性と相まって多くの分野で利用されています。
有限要素法における連成解析の例
熱-構造連成解析
固体に温度変化が生じて膨張や収縮することで応力が生じる熱応力問題や温度変化が構造物の変形に影響を与える熱変形問題を扱う場合、熱伝導解析と構造解析を連成して行います。
流体-構造連成解析(FSI、Fluid-Structure Interaction)
流体運動によって生じた圧力が構造物に作用し、それによって生じた構造物の変形が再び流体の流れに影響を与える場合、流体解析と構造解析を連成して行います。構造物の振動が起点となって流体の流れを変化させ、その流れの変化が再び構造物の振動に影響を与える場合も同じです。
電磁-熱連成解析
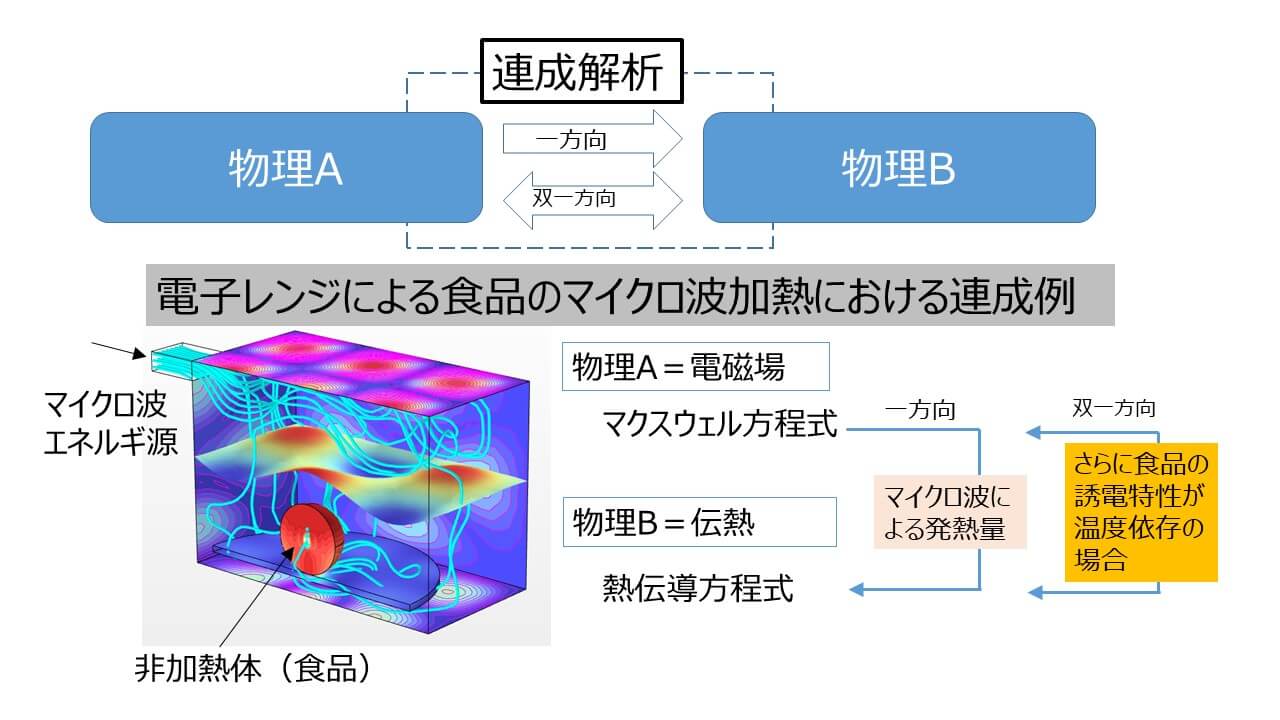
電気抵抗を持つ固体内部に電流を流したときジュール熱が発生して固体の温度が上昇しますが、固体材料の電気抵抗が温度に依存する場合には電流の解析と熱伝導解析を連成して行います。外部コイルに流す交流電流が材料内に渦電流を生じる場合には、外部コイルが誘導する材料内部の電磁場とそれによって生じる誘導加熱を発熱源とする熱伝導解析を連成して行います。電子レンジではマグネトロンから生じる電磁波が電子レンジの内壁による反射・吸収を繰り返しながら食品に入射しマイクロ波加熱による食品温度の上昇を解析するためにマックスウェル方程式を周波数領域で解き、食品内部の伝熱解析を連成して行います。食品の材料特性が温度に依存して自身の誘電特性およびマイクロ波エネルギー吸収の具合を変化させる場合にはマックスウェル方程式による電磁波解析と食品の熱伝導解析を同時に解く必要があります。通常は計算負荷を抑えるために食品外部に生じる空気の熱対流の影響は食品表面での熱伝達境界条件として扱うことで空気の熱対流解析を行いません。しかし、食品の温度が相当に高くなり、食品外部の空気の対流を促進することでその影響が無視できなくなった場合には電子レンジ庫内の熱流体解析も同時に行う必要があります。この場合にはマックスウェル方程式による電磁波解析、熱伝導解析、空気の熱伝導解析と流体解析の4つの物理の連成解析となります。
音響-構造連成解析
ギターを弾く人は音叉を叩き、その音を聞きながらギターの調弦をします。この場合、音叉が構造的な振動を生じ、その動きによって空気中の密度(圧力)変化による音波を生じ人はそれを耳で聞いています。最近はビエゾタイプのクリップチューナーを使いますが、その場合にはギターの弦が振動することでチューナーが音を検知します。従って、音叉の場合には、構造解析(振動解析)とヘルムホルツ方程式による圧力波を連成して解きます。ビエゾタイプのクリップチューナーの場合には、弦の構造方程式(振動解析)と楽器の構造解析(振動解析)、さらにクリップチューナーの圧電素子の振動解析を連成して解くことになります。
多重物理連成解析に適したソフトウェア

連成解析はその連成内容を増やしていけば確かに物理現象に忠実な計算が可能になるのは理解できます。しかし、それだけ計算コストがかかります。従って、連成の数が増えて多重物理連成(マルチフィジックス連成解析)へ進む場合には、最終的な性能に効きそうなものを選択してそれらの物理の連成解析を行い、支配的な部分の性能分析を行います。そこの理解が進んだ時点でさらに連成する物理を追加してその影響を分析するといった戦略が必要となります。連成する物理方程式によっては解くことが非常に難しいものもあります。従って、多重物理連成解析に利用するソフトウェアは、複数物理を連成させたり、いくつかの物理は非連成にしたりといった設定が自由にできるものを選ぶ必要があります。メッシュの配置は物理方程式によって変える必要も出てきます。利用するソフトウェアでは物理ごとに適したメッシュを利用できるものを選ぶことも重要なポイントとなります。
強連成と弱連成のどちらが良いか
連成解析では複数の物理を一緒に解きます。その時、「一緒に」という場合、強連成(すべての現象を同時に解く連成方式)、あるいは弱連成(分割法(Segregated method) とも呼ばれる。異なる物理現象を個別に解析しその結果を相互に利用する連成方式)という2つのタイプがあります。強連成は各物理の方程式を同時に解く方法です。連成に加える全ての物理方程式を一つの方程式系として組み込み、一度に解を求めます。この方法は解析精度が一般に高いと考えられますが、計算コスト(計算に必要なメモリ、計算時間)は大きくなります。しかし、この方法の利用は問題に応じて臨機応変に検討する必要があります。例えば、連成する物理方程式のうち、敏感な方程式を連成する場合が挙げられます。この場合、計算過程で生じるノイズに敏感な方程式はすぐにその影響を受けて発散し、計算ができなくなることがあります。
一方、弱連成では本来、同時に解くべき物理方程式の場合に分割して解くことで、一方の物理方程式に生じた変化がすぐに他方の物理方程式に影響を与えずタイミングが遅れることで全体の収束計算時間がのびることがありますが、計算メモリを多く使わないという点では多くの物理を連成して解く場合に適していると言えます。従って、強連成と弱連成のいずれがいいかという問いかけには、場合によるという答えになります。一方で強連成解析を備えていないソフトウェアは扱える問題が制限されるということは言えます。