有限要素法
- ホーム >
- COMSOL Multiphysics >
- 有限要素法
有限要素法(FEM)とは?
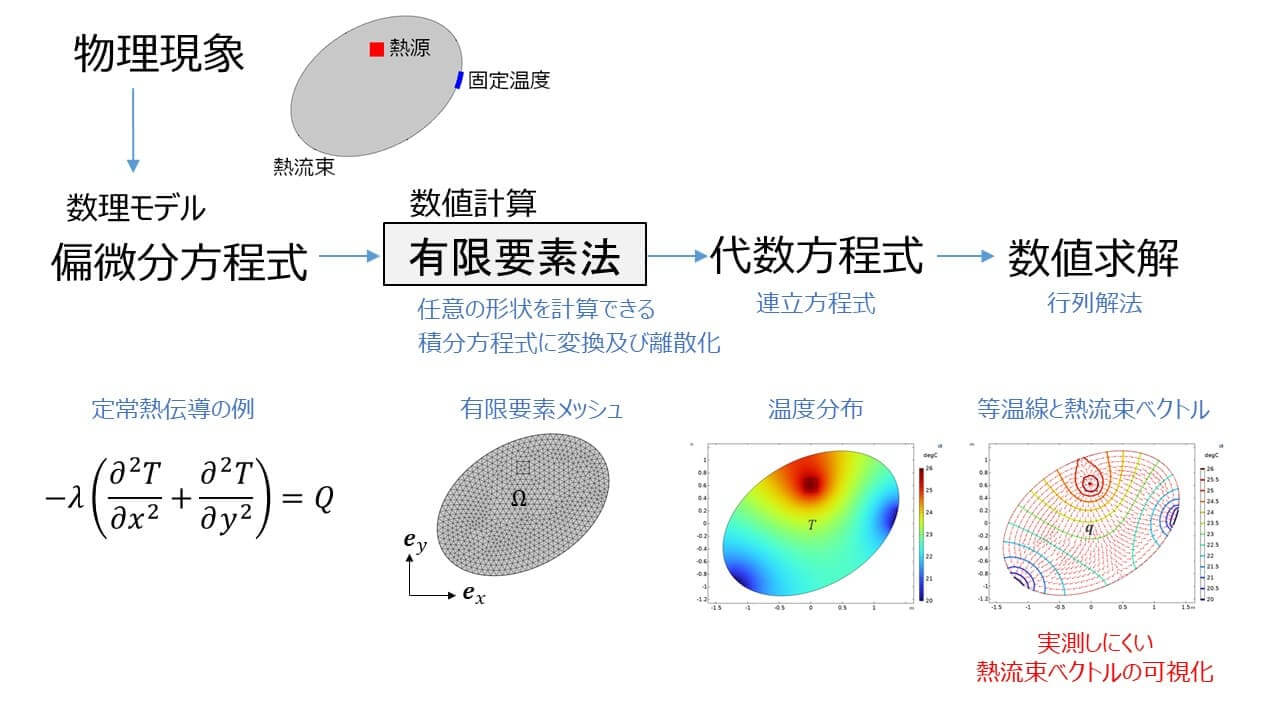
有限要素法とは、解析対象となる領域を「要素」と呼ばれる単位に分割することでその領域に生じる現象の支配方程式を数値的に解く数値解析手法です。有限要素法は支配方程式の積分形である弱形式を数値解析の対象にすることから境界条件の取り扱いが正確に行えます。有限要素法の代表的な適用例としては固体解析や構造解析が良く知られていますが、重み付き残差法の導入によって固体や構造に加えて、より一般的な現象を記述する偏微分方程式の初期値・境界値問題の汎用的解法になりました。その結果、有限要素法は伝熱解析、流体解析、マクスウェル方程式による電磁界解析、音響解析、電池解析、腐食・防食解析、プラズマ解析、土壌掘削解析、地下水流解析、化学反応流解析、生物・生体の反応拡散解析といった幅広い分野への応用が急速に進展しています。有限要素法は空間分割に関する柔軟性から複雑な形状や境界条件をもつ現象を効率的に解析できます。有限要素解析はその汎用性と柔軟性から、数理分野での偏微分方程式の数値解析といった問題から、製品開発による設計段階での予測、現場での実用的な問題解決に至るまで幅広く役立っています。
基本的な考え方
有限要素法は、次のような基本的な考え方に基づいています。
離散化とメッシュの作成
解析したい連続領域を小さな要素(有限要素)に分割し、計算機で扱える程度の離散的な問題に変換します。要素の形状には、三角形、四角形、4面体、六面体などが使われます。空間の要素分割を行う段階はメッシュ(網目)分割あるいはメッシュ作成と呼ばれます。フリーあるいは市販のソフトウェアではメッシュ分割は解析対象の形状を与えれば自動で行えるようになっています。
形状関数による空間分布の近似表現
各有限要素内の物理量(例えば構造変位や温度など)の分布を近似的に表現することを考えます。そのために形状関数(補間関数)を使います。各有限要素内の物理量(例えば構造変位や温度など)の分布は要素節点における物理量(未知数、あるいは解と呼ぶ)と、空間座標の関数である形状関数を使った補間で記述されます。後述する方程式の導出において物理量の空間座標に関する微分が必要となりますが、形状関数を空間座標で微分することで空間微分を計算できます。
弱形式と要素行列方程式
数値解析は、物理法則(例えば、エネルギー保存、力のつり合いなど)を満たさなければなりません。物理法則は時間と空間に関する偏微分で表現された物理方程式の初期値・境界値問題として記述されます。有限要素法は物理方程式から得られる積分式の形をした弱形式(Weak Form)を使って各有限要素内での未知数(問題の解)を決めます。弱形式には物理量の空間微分が含まれ、さらにそれらの積分が含まれます。空間微分と同様、積分も形状関数に基づいて計算ができるので各有限要素において未知数の数だけの代数方程式を得ることができます。これは未知数に関する要素行列方程式となります。
全体方程式の組み上げ
各要素で得られた要素行列方程式から全体方程式を組み上げます。得られる解析対象全体の全体方程式は実際的な問題においては大規模な方程式になります。
境界条件の適用
解析対象の従う物理法則は同じでも状況によっては挙動が異なる場合があります。例えば、固体力学の方程式に従う板でも一端を完全固定とするか、あるいはローラーで滑るようにするかで荷重をかけたときの板の挙動は異なります。これは境界条件が異なるからです。固体力学では固定端、自由端、荷重といった具合に名前を付けて区別しています。従って、前述の4.で求めた全体方程式は各問題特有の境界条件を満たす条件を与えた上で解を求める必要があります。
数値解法(ソルバー)
全体方程式に境界条件を課して得られた方程式系を数値的に解きます。ここで利用される数値解法はソルバーと呼ばれますが、数値解析の教科書に出ている行列解法と呼ばれるものを使います。行列解法には直接法(Direct Solver)と反復法(Iterative Solver)があり、さらに線形ソルバーと非線形ソルバーを問題に応じて使い分けます。行列解法を適用することで有限要素の各節点においた未知数が決まり、形状関数を使うことで物理量の空間分布が求まります。有限要素法では、弱形式から全体方程式系を導出する過程はルーチン化できます。各物理分野特有の工夫が必要な場合もありますが全体方程式を得るまでの大部分の導出過程は共通しており、有限要素解析が広い物理分野で汎用的に利用される所以です。
時間依存の取り扱い
時間依存の問題で、構造物の強制振動や電磁界のようにある周波数で定常的な振動をする現象は周波数領域での方程式に変換することで定常解析と同じ数値解析を行うことができます。一方、定常振動を考えない時間的過渡段階の解析をする場合には線の方法(Method of Lines)が使われます。この方法は時間方向の離散化に従来使われている差分法を利用できる利点があります。
有限要素法のメリット
複雑な形状の取り扱いが容易
機械部品、人体、自動車、航空機、船舶、宇宙船、建築物、地形、地球表面といった様々な形状を有限要素で容易に取り扱える。
計算規則の共通性
重み付き残差法の適用によって任意の偏微分方程式の初期値・境界値問題を同じ形式の離散方程式に帰着させることができ、計算規則も共通化できる。
マルチフィジックス解析に適している
様々な物理を有限要素で離散化し共通の計算規則を使えるので流体-構造、音響-構造、電磁気-伝熱といった多重物理連成解析(マルチフィジックス解析)に適している。
有限要素法のデメリット
計算機の使用メモリ量が多い
有限要素法は解析対象を有限要素(メッシュ)に分割するが、偏微分方程式に含まれる空間微分項を計算するには形状関数が必要である。有限要素法は有限要素の節点(高次要素では中間節点も利用)に配置した未知数と形状関数による近似解を構成する。有限要素のサイズを小さくして行けば正解に近づくとされているが、解析対象によってはかなり細かな有限要素を配置する必要があることから、計算機の使用メモリ量を数多く必要とする。
有限要素の寸法設定や配置に経験が必要
取り扱う物理によるが、有限要素の大きさや配置については経験が必要である。市販のソフトウェアであれば自動的に有限要素の寸法や配置を決めるものがあるが、自動メッシュ設定を使うとメッシュ数が多くなってしまう傾向がある。使用可能な計算メモリ量を超えてしまうと計算実行ができなくなるので、手動でメッシュを作成することがあり得る。その場合にはメッシュの数を減らしつつ必要な計算精度を確保するといった経験が必要となる。
利用分野
有限要素法は以下のような様々な分野で利用されています。
構造解析
- 弾塑性力学
- 土壌力学
- コンクリート
- マルチボディダイナミクス
熱解析
- 熱伝導
- 対流放射伝熱
- 生体伝熱
流体解析
- 非圧縮性
- 圧縮性
- 乱流
- 多相流
- 地下水流
電磁場解析
- 高周波電磁界
- モータ・回転機械
- 静電気・静磁気
- 電気回路
音響解析
- 音波
- 超音波
- ハイブリッド計算出力音響(ライトヒル アナロジー及びAWEアナロジー)
化学反応工学・電気化学解析
- 電気化学反応
- 全固体電池
- 燃料電池
- リチウムイオン電池
- 腐食
- めっき
- 化学反応
半導体解析
- IGBT
- 太陽電池
- InAs ナノワイヤ
- MOSCAP
- バイポーラトランジスタ熱解析
プラズマ解析
- 容量結合性プラズマ
- 誘導結合性プラズマ
- 誘導結合性プラズマ(RFバイアス)
数理科学
- COVID-19
- 粘菌
- 食品
- DNAナノポア
- ブラック・ショールズ方程式