数理工学と応用数学

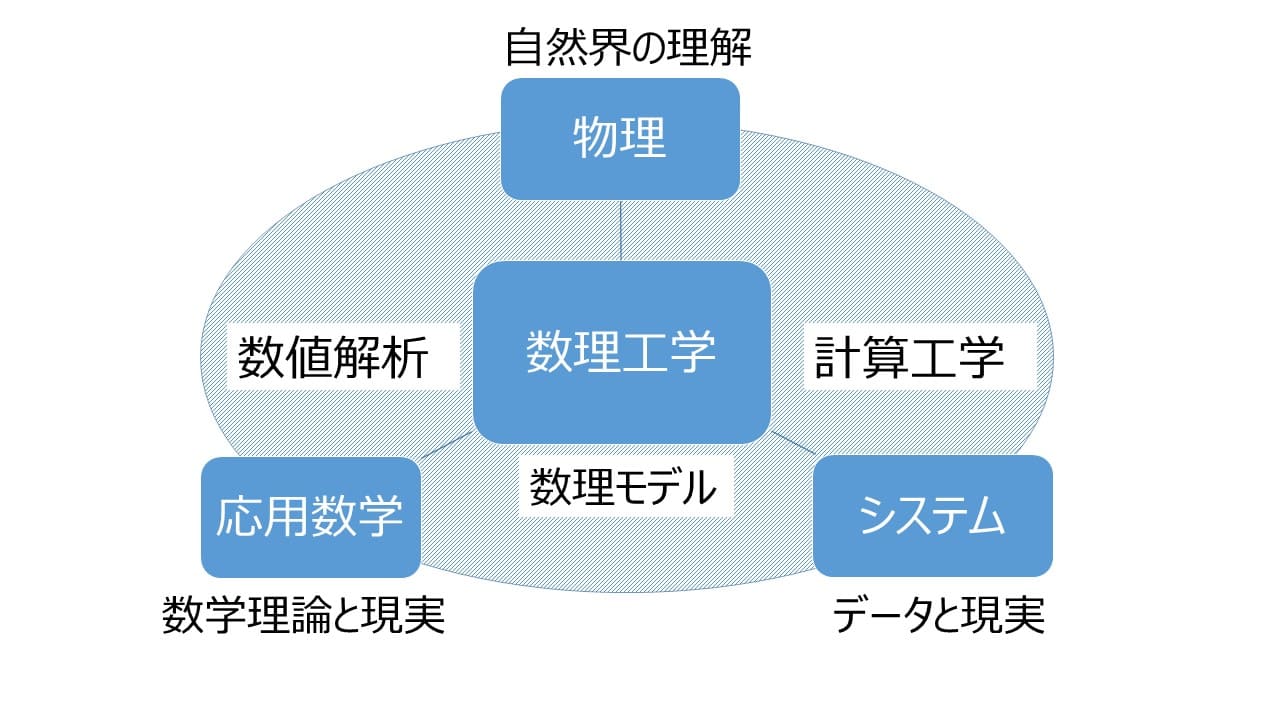
数理工学は数理モデルと計算技術を用いて工学的な問題を解決する学問です。そこではコンピューターを使った数値シミュレーションが行われます。数理モデルは、現実のシステムや現象を数学的な形式で表現するものです。数理モデルは一般に微分方程式（常微分方程式や偏微分方程式）が用いられます。数理モデルによる解析では数理モデルを表現する数式の計算や方程式の数値解を求める必要があり、それには数値解析が必要です。数値解析とは実務家では主に現象に数値的手法を適用して解析・解明するという意味に用いられ、数学的な問題をコンピューターによって解くための方法論や技術のことと捉えています。数学者やその周辺では数値計算法の原理や得られる数値解の挙動を数理的に解明することを意味するといった具合で、立場によって言葉の意味も変化することを覚えておく必要があります。応用数学（Applied Mathematics）は数学的な理論と手法を現実世界の問題に適用する学問分野で近似理論である数値解析を含んでいます。応用数学は自然科学や工学での適用から、近年では、経済学、社会科学、神経科学、医療と多岐にわたっています。神経科学からはニューラル・ネットワークの理論が生まれています。

CAE(シー・エイ・イー、計算機援用工学、Computer-Aided Engineering)は数理工学の理論と手法を広く応用していますが、CAEでは設計での問題解決を図ることが最重要課題であり、機能や性能の検討、さらに製品を製造するための成形性や加工性の検討も含まれてくるところに違いがあるとされています。CAEの課題は高度化しており、流路の最適化などでは生物模倣（Biomimetics）による自動設計といった数理工学の知識の活用も行われています。CAEでは計算負荷や予測に要する時間の短縮といった課題も生じており、ディープ・ニューラル・ネットワークによるサロゲートモデルの利用やトポロジー最適化といった応用数学の成果をどんどん取り入れています。 このように、数理工学、応用数学はお互いに補完する関係にあるようです。CAEという工学的問題を解決する立場ではそれらの成果をうまく活用することが大切です。CAEと実測との比較検証を通じて未知の課題に出くわしたら、それを数理工学、応用数学の面から検討を加えて解決を図る作業も大切なことです。それをきっかけとして数理工学と応用数学が発展し、新しいCAEの手法やアルゴリズムの開発を促進し、それがエンジニアリングのイノベーションを推進するでしょう。

以下で、数理工学のプロセスがどのようなものか一例を示します。数理工学は工学問題毎に方法を考えるのではなくて問題に潜む共通の構造を抽象化した数理モデルを使って問題解決のための普遍的な方法を見出すといったようないろいろな考え方があり、それに応じてプロセスも異なりますので一つの考え方として理解してください。