BLOG
KESCOブログ
モノづくりと不確かさの定量化（第7回）ガウス過程回帰
7 ガウス過程回帰
前回、ガウス過程はランダムな関数を発生する確率分布\(\ {\bf f} \sim {\cal N}(\BS(\mu) ,K)\ \)であることを紹介した。共分散行列\(\ K\ \)の要素を与えるカーネル関数と平均関数\(\ \BS(\mu) \ \)が与えられると、関数\(\ f \ \)の事前分布としてガウス過程が定まることになる。ここで、線形回帰モデルの場合と同様に観測データ集合\(\ {\cal D}\ \)を与えると\(\ f\ \)の事後分布を求めることができる。今回はこのシナリオに従って、ガウス過程に基づいた回帰モデルであるガウス過程回帰（Gaussian process regression, GPR）を紹介する。
7.1 ガウス過程回帰モデルの導出
ガウス過程に基づいて回帰問題を解くことを考える。線形回帰モデルの場合と同様に、\(\ N\ \)個の観測値
\[ {\cal D} = \{\,({\bf x}_i,y_i)\,|\, i = 1, \cdots ,N\, , \,{\bf x}_i \in {\cal X}\, ,\,y_i \in \RR \}\tag{7.1}\]
が与えられているとし、以下の４つの前提を考える。
(１) 出力 \(\ y\ \)の平均は\(\ 0\ \)に正規化されている。
(２) 入力\(\ {\bf x}\ \)と出力\(\ y\ \)の間に\(\ y=f({\bf x})\ \)の関係がある。
(３) 関数\(\ f\ \)がガウス過程\(\ f \sim {\cal GP}\,({\bf 0},k({\bf x},{\bf x}’))\ \)から生成されている。
(４) 出力\(\ y\ \)には\(\ {\cal N}(0,\sigma_n^{\,2})\ \)に従うノイズが重畳している。
このとき、\(\ {\bf y}=(y_1,y_2,\cdots ,y_N)\TP \ \)は、カーネル関数\(\ k({\bf x}_i\,,{\bf x}_j)\ \)を用いて
\[ K_{ij}=k({\bf x}_i\,,{\bf x}_j)+\sigma_n^{\,2}\delta_{ij} \tag{7.2}\]
で与えられるカーネル行列\(\ K\ \)を共分散行列とするガウス分布に従う。
\[ {\bf y} \sim {\cal N}\,({\bf 0},K) \tag{7.3}\]
以上が、前回のガウス過程の紹介した内容のまとめである。
7.2 ガウス過程回帰の予測分布
前述の前提に基づいて、観測点に含まれないテスト入力\(\ ({\bf x}_1^*,{\bf x}_2^*,\cdots ,{\bf x}_M^*)\ \)における出力\(\ (y_1^*,y_2^*,\cdots ,y_M^*)\ \)を求める回帰問題を解く。線形回帰モデルの場合には、重みパラメータによって \[ y^*={\bf w}\TP \BS(\phi) ({\bf x}^*) \tag{7.4}\] と予測することができた。しかし、ガウス過程の場合には、既に\( \ {\bf w}\ \)は積分消去されているので式 (7.4) による予測は行えない。しかし、観測値\(\ {\bf x}\ \)とテスト入力\(\ {\bf x}_*\ \)から得られる\(\ (N+M) \times (N+M)\ \)次元のカーネル行列を\(\ K’\ \)とすると \[ (y_1, \cdots, y_N, y_1^*, \cdots, y_M^*)\TP \sim {\cal N}({\bf 0},K’)\] が成立するのがガウス分布の重要な性質である。ここで、以下のように観測値とテスト入力を略記することにする。 \begin{cases} X&=&({\bf x}_1,{\bf x}_2, \cdots ,{\bf x}_N) \\ X_* &=&({\bf x}_1^*,{\bf x}_2^*, \cdots ,{\bf x}_M^*) \\ \,{\bf y}&=&(y_1,y_2,\cdots ,y_N)\TP \\ \tag{7.5} \end{cases} また、テスト入力に対する予測値ベクトルを \[ {\bf f}_* =(f({\bf x}_1^*),f({\bf x}_2^*), \cdots ,f({\bf x}_M^*))\TP \tag{7.6} \] と表し、\(\ {\bf y}\ \)と\(\ {\bf f}_*\ \)の同時分布 \[ \begin{pmatrix} {\bf y} \\ {\bf f}_* \end{pmatrix} \sim {\cal N}\left({\bf 0}\, , \begin{pmatrix} K & K_* \\ K_*\TP & K_{**} \end{pmatrix} \right) \tag{7.7}\] を考える。
ここで、\(\ K_*\ \)は\(\ k({\bf x}_i,{\bf x}_j^*) \ \)を\(\ i,j\ \)成分とする\(\ N \times M\ \)行列、\(\ K_{**}\ \)は\(\ k({\bf x}_i^*,{\bf x}_j^*) \ \)を\(\ i,j\ \)成分とする\(\ M \times M\ \)行列である。
式 (7.7) から\(\ {\bf f}_*\ \)の事後分布を求めることは、\(\ {\bf y}\ \)が与えられたもとでの条件付き分布を求めることと等価であるので、以下の公式を適用することができ、式 (7.8) の事後分布が得られる。
［公式］多変量正規分布の条件付き分布
\begin{eqnarray}
{\bf x}=\left( \begin{array}{c} {\bf x}_1 \\ \hdashline {\bf x}_2 \end{array} \right) \sim
{\cal N} \left(
\left( \begin{array}{c} \BS(\mu) _1 \\ \hdashline \BS(\mu) _2 \end{array} \right)\,,\,
\left( \begin{array}{c:c} \Sigma_{11} & \Sigma_{12} \\ \hdashline \Sigma_{21} & \Sigma_{22} \end{array} \right)
\right)
\end{eqnarray}
のとき、
\[ p\,({\bf x}_2\,|\,{\bf x}_1)\sim {\cal N} (\BS(\mu) _2 +\Sigma_{21} \Sigma_{11}^{-1}({\bf x}_1-\BS(\mu) _1)\, , \,\Sigma_{22}-\Sigma_{21} \Sigma_{11}^{-1}\Sigma_{12}) \]
\[p\,({\bf f}_*\, |\, X_*\,,{\cal D})={\cal N}\, (K_*^{\,\intercal} K^{-1}{\bf y},\,K_{**}-K_*^{\,\intercal} K^{-1}K_*) \tag{7.8}\]
出力\(\ {\bf y}\ \)には、ノイズ\(\ {\cal N}({\bf 0},\sigma_n^{\,2}) \ \)が重畳しているので、最終的に出力\(\ {\bf y}\ \)の予測分布は次式で与えられる。
\[p\,({\bf y}_*\, |\, X_*\,,{\cal D})={\cal N}\, (K_*^{\,\intercal} K^{-1}{\bf y},\,K_{**}-K_*^{\,\intercal} K^{-1}K_*+\sigma_n^{\, 2}I_M) \tag{7.9}\]
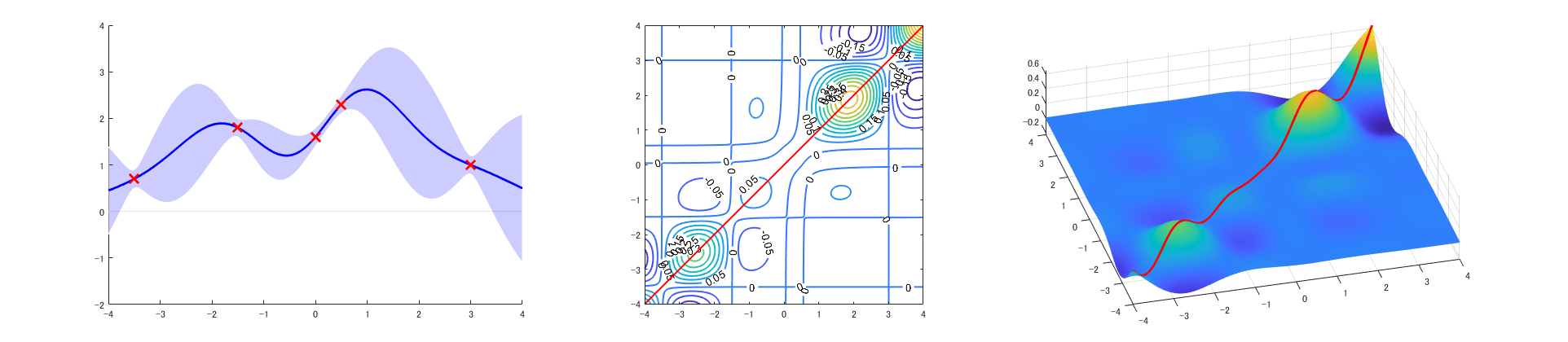
図 7.1 に前回紹介した１次元観測値のガウス過程回帰の例を再掲する。カーネル関数は次式で\(\ \theta_1=1\,,\theta_2=1\ \)とするの動径基底関数を適用し、さらにノイズの分散は\(\ \sigma_n^{\,2}=0.01\ \)とした。また観測データとして x 印の５点を与えた。 \[k({\bf x},{\bf x}’)=\theta_1 \exp \left( -\frac{|{\bf x}-{\bf x}’|^2}{\theta_2}\right) \tag{7.10}\] 区間\(\ [-4,4]\ \)を等間隔\(\ 0.01\ \)で刻んだ\(\ 801\ \)点をテスト入力とし、式 (7.9) により予測分布を求めた。図 7.1 に求めた共分散行列を等高線表示（中央）、３次元表示（右）し、赤色の線が入力点\(\ x\ \)における分散\(\ \sigma^2(x)\ \)を表している。また、等高線図からテスト入力点間で分散の符号が変わる（正の相関か負の相関に相当）領域を読み取ることができる。図 7.1（左）は、予測分布に平均値（青色の線）と信頼区間95%（平均値\(\pm 2\sigma\)）の領域を示した。
同じカーネル関数を用い、以下の手順で求めた２次元データの予測分布の事例を動画 7.1 に紹介する。
- 50組の2次元のデータ\(\ (x_1,x_2) \ \)を区間\(\ -1 \le x_1,x_2 \le 1\ \)の範囲でランダムに発生させる（右側のｘで示す）。
- 関数\(\ f(x_1,x_2) = \exp( -(2x_1^{\,2} + 2.5x_1x_2 + 3x_2^{\,2}) )\ \)によって観測値を求める。
- 観測値のペアを5組から50組まで変化させ、式 (7.2) によって共分散行列を得てガウス過程に従う事前分布を求める。そして、区間\(\ [-1 ,1]\ \)を等間隔に\(\ 0.05\ \)で刻んだ\(\ 41 \times 41 = 1,681\ \)点のグリッドをテスト入力とし、式 (7.8) で事後分布を求める。
より高次元のデータについてもガウス過程回帰による予測分布を求めることは可能であるが、予測分布を可視化することは困難である。
7.3 カーネル関数
これまでは、カーネル関数として動径基底関数を用いてきたが、その他のカーネル関数も提案されている。代表的なものを以下に紹介する。
- 線形カーネル \[ k({\bf x},{\bf x}’)={\bf x}\TP {\bf x}’\]
- 指数カーネル \[ k({\bf x},{\bf x}’)=\exp\left(-\frac{|{\bf x}-{\bf x}’|}{\theta}\right)\]
- 周期カーネル \[ k({\bf x},{\bf x}’)=\exp\left(\theta_1\cos\left(\frac{|{\bf x}-{\bf x}’|}{\theta_2}\right) \right)\]
- マターンカーネル（Matérn kernel） \[ k_\nu({\bf x},{\bf x}’)=\frac{2^{1-\nu}}{\Gamma(\nu)} \left(\frac{\sqrt{2\nu}\,|{\bf x}-{\bf x}’|}{\theta} \right)^\nu\ K_\nu \left(\frac{\sqrt{2\nu}\,|{\bf x}-{\bf x}’|}{\theta} \right)\]
7.4 まとめ
ガウス過程回帰によって観測値から自由度が高く柔軟な関数の確率モデルを求める手順を紹介した。しかし、図 7.1 や動画 7.1 の予測分布を求める際には、カーネル関数のパラメータ\(\ \theta_1,\theta_2\ \)を固定した。このパラメータを線形回帰モデルの場合の重みパラメータとは異なることからハイパーパラメータ（hyperparameter）という。次回は、選択の自由度のあるハイパーパラメータをどのように推定すればより良い予測分布が得られるかという問題について紹介する。 前回までの連載一覧
●モノづくりと不確かさの定量化（第6回）ガウス過程
https://kesco.co.jp/blog/3876/
●モノづくりと不確かさの定量化（第5回）線形回帰モデルと確率モデル
https://kesco.co.jp/blog/4426/
●モノづくりと不確かさの定量化（第4回）線形回帰モデル
https://kesco.co.jp/blog/3844/
●モノづくりと不確かさの定量化（第3回）回帰モデルの導入
https://kesco.co.jp/blog/3171/
●モノづくりと不確かさの定量化（第2回）
https://kesco.co.jp/blog/3092/
●モノづくりと不確かさの定量化（第1回）
https://kesco.co.jp/blog/539/