PRODUCT SMART UQ
不確かさ伝播
不確かさ伝搬を利用して、不確実な入力を出力確率にトレースします。
不確かさ伝播は、予想される入力にばらつきがあった場合に、システムの出力が要求を満たすかどうかを判断するのに役立ちます。これにより、結果の確率を推定し、必要な許容範囲をコスト効率よく決定し、より多くの故障を事前に予測することが可能になります。
SmartUQは、高度な確率論的数学を使いやすいツールで提供し、エミュレータベースと一般化多項式カオス展開(gPCE)の2つの方法で不確かさの伝播を計算することができます。
不確かさ伝播とは?
不確かさ伝播は、システムの各入力に関連する不確実性に基づいて、システムの出力の不確かさを計算します。すべてのモデル、予測、測定には不確かさが伴います。初期条件、環境パラメータ、測定誤差など、さまざまな入力の不確かさは、シミュレーションやテストの結果に予想外の影響を与える可能性があります。
シミュレーションやテストの結果に含まれる不確かさの原因と規模を知ることは、設計や意思決定が間違っていないかどうかを判断する上で非常に重要です。このように、不確かさの伝播は、重要な意思決定のための確かな根拠を提供するための重要なツールとなります。
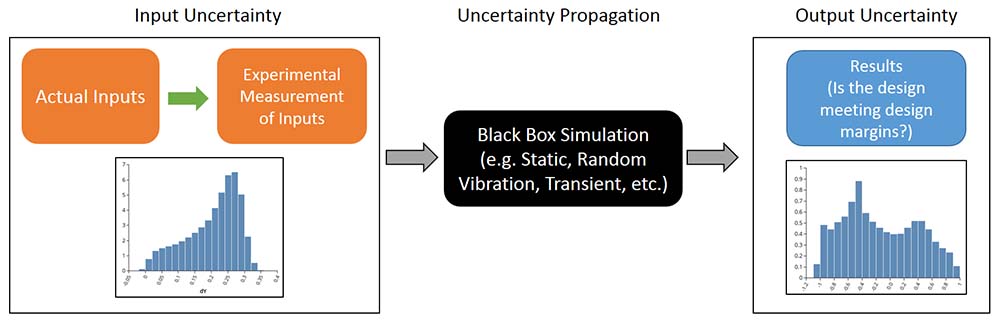
図1:不確かさの伝播フロー
シミュレーションによる不確かさの伝播の計算における典型的なデータフロー
エミュレータベースの不確かさ伝播
従来、不確かさ伝播の結果は、モンテカルロ法などの大規模なDOEを用いてシステムの入力を実行し、出力の挙動を観察することで計算されていました。しかし、大規模かつ高次元の問題では、必要なDOEのサイズが非常に大きくなり、不確かさの伝播を計算するには法外なコストと時間がかかってしまいます。
エミュレータを使用した不確かさ伝播則の計算は、サンプリングを多用する手法よりも速度が向上するため、一般的なソリューションとなっています。しかし、大規模で複雑なデータセットを用いてエミュレータを構築することは計算上困難であるため、多くがエミュレータの使用は小さな問題に限られていました。 SmartUQの画期的な技術を使えば、大規模な問題でもエミュレータを使った不確かさの伝播がわずか数クリックで可能になります。SmartUQの直感的なツールを使えば、事前に構築したエミュレータを使って、確率分布や、予想されるシステムの動作条件や記録されたテストなどの既存の入力パラメータセットを使って、不確かな入力を素早く定義することができます。
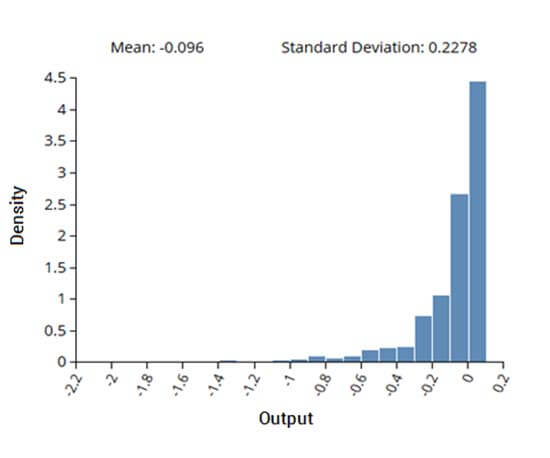
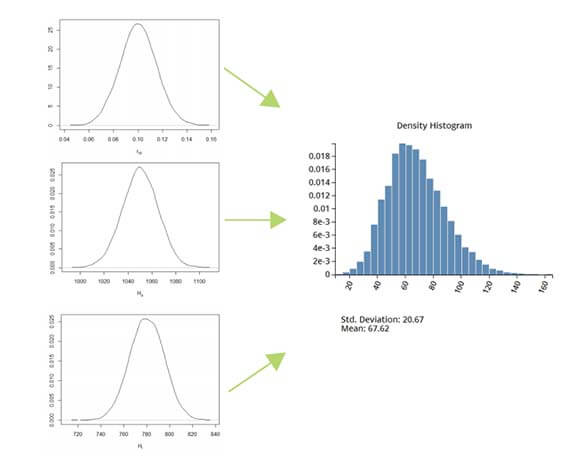
図2:エミュレータベースの不確かさ伝播
この例では、エミュレータを構築し、3つの入力変数と1つの出力変数で構成されるシミュレーションデータセットの不確かさ伝播を計算するために使用しました。入力変数には、予想される不確かさに基づいて確率分布が割り当てられました。割り当てられた入力分布をもとに、計算された出力の確率密度分布を上に示します。
不確かさ伝播のための一般化された多項式カオス展開
SmartUQには、使いやすい一般化多項式カオス展開(gPCE)ツールが搭載されています。gPCEは、多変量多項式の系列を用いてシステムの挙動を推定する応用数学の手法です。評価対象となるシステムをスパースグリッドDOEを用いてサンプリングし、gPCEを用いて、確率的出力とそのランダムな各入力との間の関数的関連性を近似します。gPCEは、スパースグリッドDOEに必要なポイント数が少なく、結果の計算速度の点でも、非常に効率的な手法です。
gPCEの出力は、多変量多項式の系列として記述することができます。多変量多項式は、それ自体が一次元多項式で構成されています。各一次元多項式は、異なる連続的な確率分布の種類に対して、最適な基底関数を提供します。各基底関数の最適性は、連続分布の確率密度関数に対する直交性に由来します。
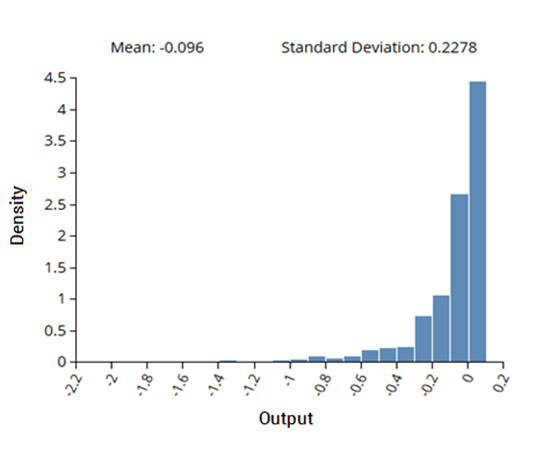
この例では、5つの入力変数と1つの出力変数からなるデータセットの不確かさ伝播を計算するために、gPCEに基づく手法が使用されました。入力変数の確率分布は、予想される不確かさに基づいて予測され、これを用いてスパースグリッドDOEが生成されました。その後、DOE を用いてシステムを評価し、その結果得られた出力を gPCE解析に使用しました。入力の確率分布から計算された出力の密度分布を左に示しています。