PRODUCT SMART UQ
不確かさの定量化の概要
定義
不確かさの定量化(Uncertainty Quantification: UQ)は不確実性定量化、UQ解析とも呼ばれていますが、計算工学や実世界のシステムにおける不確かさを定量化すること、すなわち統計的に特徴づけ、要因の特性を明らかにし、観察した結果から法則や事実を推論する帰納モデルによって確率的に予測することです。
UQは、不確実性を持つ現象、つまり実世界のばらつきや確率的なふるまいをエンジニアリングやシステム分析や評価手法に組み込むことを目的としています。通常の数値解析のようなシミュレーションや試験は、通常以下のような質問に答えるものです。「システムに単一のある入力を与えたときに何が起こるか?」
しかしUQはこの問いを発展させ、次のように問いかけます。「システムが不確実で、ゆらぎのある世界、つまり変化しうる入力範囲や分布を持っている場合に、何が確率的に起こりえるか?」ということです。
不確かさの定量化(UQ)の背景
UQは、数学、統計学、エンジニアリング領域が交わる分野からスタートしました。これらの多様な分野から、研究対象となるシステムの内部構造に関する知識を必要せず、またシステムに依存しないこれらの強力なUQ手法が生まれました。つまりUQの手法を利用するには入出力の応答動作に関する情報のみだけで十分です。そのため、エンジニアリングシステムで有効な手法は、同様のふるまいを示す金融問題にも同様に適用できる可能性があるということです。これにより、今後もますます多くの産業がUQの進歩の恩恵を受けることができるようになるでしょう。
なぜ「不確かさの定量化」なのか?
UQの手法は、これまで答えの出なかった多くの疑問に答えることができるため、さまざまな業界のエンジニアやモデリングの専門家に急速に採用されています。これらの手法により、以下のことが可能になります。
- ほとんどすべてのシステムに内在する不確かさの理解
- ばらつきのある実験・実測データを使って決定論的なモデルに対するデータ同化(キャリブレーション)
- 予測に対する信頼性の定量化
- 広範囲の入力に対してロバストな最適ソリューションの発見
- 開発期間、試作コスト、および予期せぬ故障の削減
- 確率論的設計プロセス(確率的シミュレーション)の導入
なぜ今なのか?
コンピュータの性能が向上し、シミュレーションやテストがより高度になるにつれ、より多くの実世界のシステムに対して正確な予測を行うことができるようになりました。現在、エンジニアリング設計の競争領域は、不確かな入力を受けたときのシステムの挙動を素早く予測することに移っています。モンテカルロ法のようなランダムサンプリングでは、膨大な数のシステムバリエーションを生成して評価する必要があります。大規模な問題では、このような方法では対応できません。
SmartUQに搭載されているような最新のガウス過程回帰の手法は、小規模なシステムでの不確実性を定量化(UQ)するだけでなく、大規模なシステムでも実現可能にしました。不確かさを含んだエンジニアリングプロセスを始めるのにこれほど良いタイミングはないでしょう。
不確実性の原因と種類
不確かさとは何か?
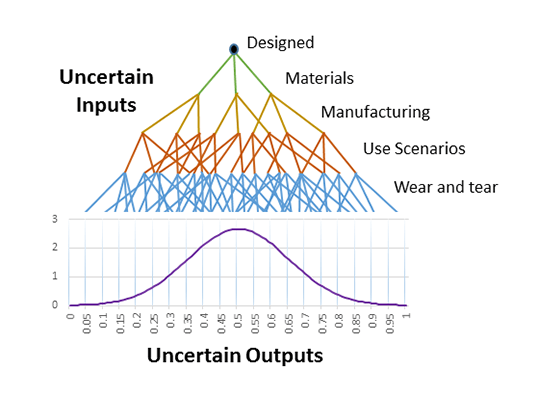
図1:不確かさが生じる仕組み
1つの出力に対して、多くの不確かさの要因が影響を与えることがあります。この図では、ある部品の予測される性能は、当初の設計値を中心とした正規分布に沿っています。
不確かさの種類
不確かさには、大きく分けて「偶然的不確かさ」と「認識論的不確かさ」の2種類があります。
偶然的不確かさ
偶然的不確かさとは、より多くの情報を集めたとしても低減することができない不確かさのことです。このような不確かさは、システムに固有のものと考えられ、確率分布で表現するのが最適です。この種の不確かさの例としては、サイコロを振った結果や放射性崩壊などがあります。
認識論的不確かさ
認識論的不確かさとは、理論的には知ることができても、現時点では入手できない情報があるために生じる不確かさのことです。したがって、認識上の不確かさは、正しい情報を収集することで低減できると考えられますが、そのための費用や困難さのために低減できないことがよくあります。この種の不確かさの例としては、ロット毎の材料特性、製造寸法、負荷のばらつきなどがあります。
シミュレーションと実験における不確かさの一般的な原因
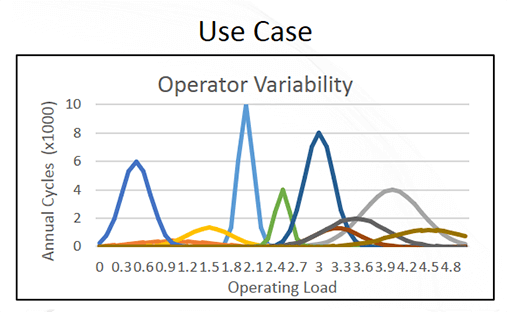
図2:不確かさの下でのシナリオ
この図は、さまざまなオペレーターのツール使用状況を示しています。1人のオペレーターが使用する個々のツール間のばらつきにより、各オペレーターに分布が生じています。また、オペレーター間でも大きな違いがあります。
不確かな入力
これは多くの場合、動作条件、設計形状および構成、負荷条件、天候、および人間の操作による入力に当てはまります。不確かな入力は、理論的には一定であったり、既知の関係に従っていたりしますが、何らかの不確かさを内在している場合もあります。
これは、測定された入力、製造公差、材料特性のばらつきなどの場合によく見られます。
モデリングフォームとパラメータの不確実性
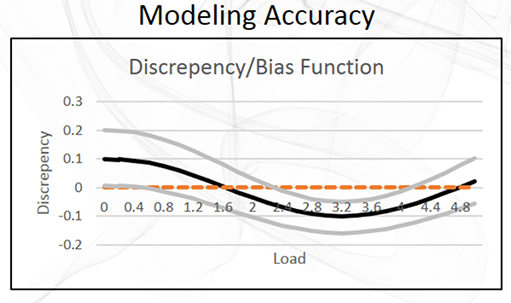
図3:不一致関数
モデルフォームの不確かさは、不一致関数で表されることがあります。これらの関数は、モデル化された結果と物理的な結果の間の予測される差を、両者に内在する不確かさを含めて与えます。
重力を例にとると、ニュートンの重力モデルにはモデル形式の誤りがあり、それが一般相対性理論によって修正されました。そのため、ニュートン重力モデルによる予測には、モデル形式の不確かさが存在します。重力加速度などのパラメータに不確かさや誤差があります。この不確かさは、多くの場合、物理的特性の測定または推定における誤差の結果であり、より多くの情報が得られるようになったときに、キャリブレーションを使用して関連するパラメータを調整することで低減することができます。
計算および数値の不確かさ
物理試験の不確定性
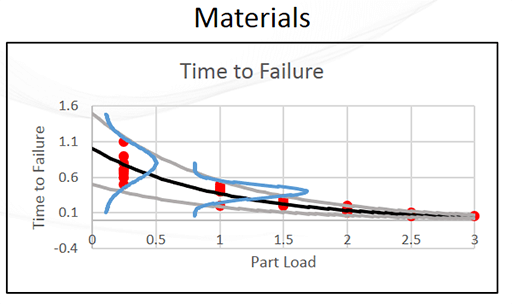
図4:テストのばらつき
同一の故障試験の間のばらつきは、物理的なシステムに内在する不確かさを示しています。